Math Members in Science
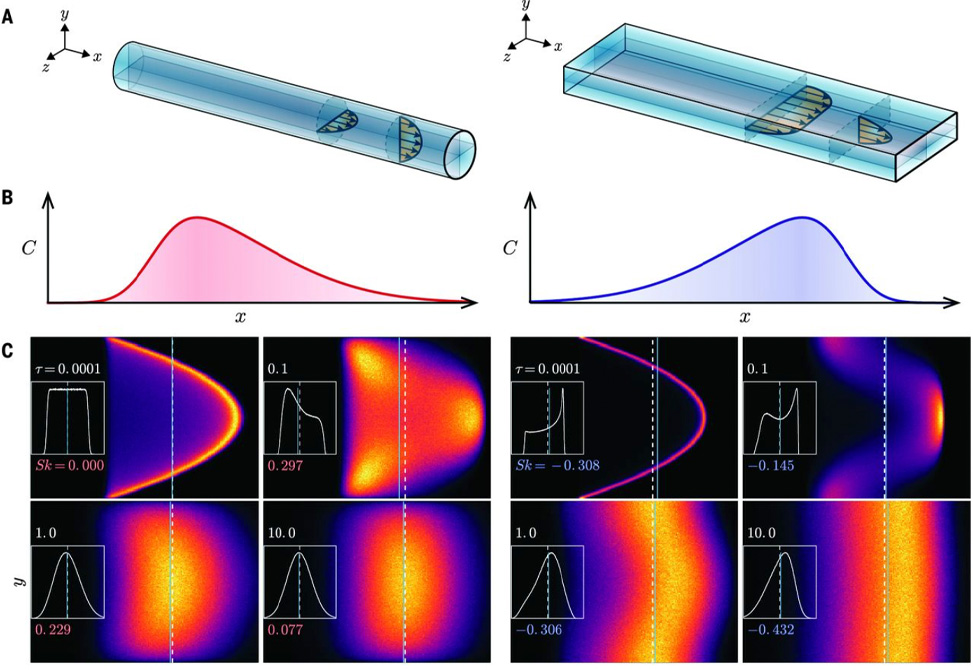
Solute is flowing from left to right in a square and skinny duct. The square case arrives with a gentler buildup, while the skinny case arrives with a more abrupt, sharper front.
Art was created with proportions in mind so spaces would make mathematical sense. Now two mathematicians from the University of North Carolina at Chapel Hill and their team have created art of their own: a method that precisely sculpts how fluids spread chemicals as they travel to hit their target.
The work, which appeared in the November 17, 2016, advance online issue of Science, has profound implications in fields such as medicine, chemistry and environmental management. Anywhere where having the ability to precisely control how drugs, chemicals and pollutants approach their destination is potentially critical for optimizing their effect, potency and lifespan.
“You might want a chemical, for example, to hit its target all at once or you might want it to build up gradually,” said McLaughlin, chair of UNC-Chapel Hill’s department of mathematics. “Until now, scientists had little control on the exact way for a chemical to do that. This work gives them a simple method so that they can achieve either of these goals — or anything in between.”
McLaughlin and his colleague, Roberto Camassa, Kenan Distinguished Professor of Mathematics, revealed that the secret to such control lies solely in the relative dimensions of the tube, not the properties of the fluid or the chemical dissolved within it. Specifically they showed that the relationship between a pipe’s width and height — or aspect ratio — governs the shape of the chemical spread as it flows with the fluid down the tube.
A circle and square are just as wide as they are tall, while an ellipse and rectangle are wider in one dimension than the other. By squishing the tube away from being a perfect circle, the researchers showed that they can change the way that a solute reaches its target: Solute traveling down a skinny pipe barrages its target fast, but if the same solution travels down a fat pipe, the solute crawls slowly upward to its target until the big punch hits at the end.
They found that precisely the same effect occurs in rectangular ducts, such that in skinny ones, solute arrives at the target strong, like a heavy punch; if you stretch the rectangle into a square, the solute reverses its approach, arriving in a slow and gradual upward swing.
“That was the big surprise,” said Camassa. “We stumbled upon this incredible disconnect between two different geometries. It’s one of nature’s universal principles governing the shape of solute spreading and it can be used to optimize results in many industries that deal with chemicals dissolved in fluid flows.”
The implications reach far and wide, particularly in microfluidic devices, which contain miniaturized components for routing and processing very small amounts of fluids. They are used in health care for making small, biological test kits or for precisely manufacturing drugs. This new work can be used to optimize microfluidic devices for any particular goal. For example, researchers can potentially optimize the delivery of cancer drugs or antibiotics to minimize damage to surrounding tissues and thus minimize side effects.
Economics also play a big role, explained McLaughlin and Camassa, who are both in UNC-Chapel Hill’s College of Arts and Sciences.
Precision elliptical pipes may be difficult and expensive to manufacture. But the new work shows that rectangular pipes, which are easier and cheaper to produce, can do the same job, delivering a fluid with calculated precision given the right aspect ratio. As a bonus, rectangular ducts stretch solute much less than ellipses, an effect that can be important in delivering more highly concentrated substances, another factor when considering cost and shape of a pipe.
The team, including graduate students Manuchehr Aminian and Francesca Bernardi, and postdoctoral scholar Daniel Harris, has revealed one of nature’s universal principles governing how fluids spread solute in microfluidic environments.
“It’s sort of a slam dunk, having analysis, computation and experiment, all these approaches confirming each other,” said McLaughlin. “It says that this phenomenon is really there and can be used for far-reaching applications.”
Story by Thania Benios, UNC Communications
